Here is something that always bugged me about the way Bayes’ Theorem is taught (esp. from the perspective of inferential statistics).
I usually see Bayes’ Theorem stated as: \[ P(A|B) = \frac{P(B|A)P(A)}{P(B)}. \] This is correct, but not indicative of anything. Let’s replace the letters with something more speaking, like \(M\) for Model instead of \(A\), and \(D\) for Data instead of \(B\): \[ P(M|D) = \frac{P(D|M)P(M)}{P(D)}. \] That is already somewhat better: We usually want to see how likely a certain model is given an observation. The right hand side to me implies a certain chunking:
- Compute \( P(D|M)P(M) \),
- then divide it by \(P(D)\).
When I read this, I’m drawn towards this mental model that is essentially about joint probabilities:
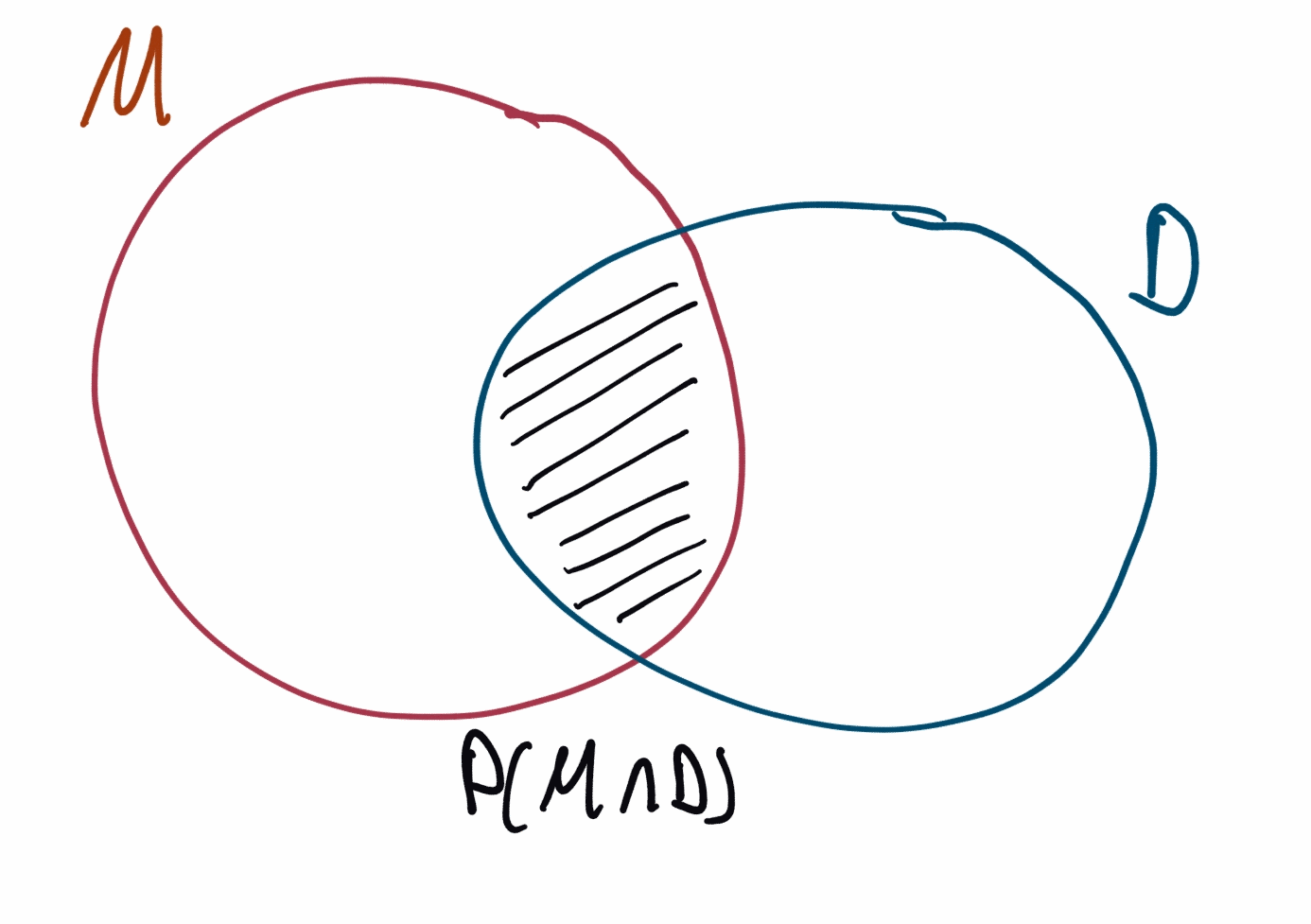
- I imagine a diagram where \(M\) and \(D\) are regions, and
- the term \(P(D|M)\) is computed as a ratio of areas, \(\frac{P(M \cap D)}{P(M)}\).
Yes, this is correct. But I find it neither helpful nor does it model how I use the theorem. Even the mental gymnastics required to make intuitive sense of \(D \cap M\) seem wasteful.
I prefer to write Bayes’ Theorem like this:
\[ P(M|D) = P(M) \frac{P(D|M)}{P(D)}. \]
This still is the same mathematical statement but it emphasises another perspective by grouping the terms differently:
- We group \(\frac{P(D|M)}{P(D)}\) together, which tells us how much more likely the data is assuming this model \(M\) compared to \(D\)’s base-rate \(P(D)\) (i.e. the average probability across all models).
- This is saying that the posterior is the prior times how much more likely the data is using this model vs. what we’d expect on average.
I find that in software engineering and programming plenty of time is spent discussing form and how to choose the proper ‘abstraction’ for a concept, how to make it elegant, etc. but I can only recall a single instance where I had a heated discussion about how a proof or theorem should be written down.
The proper presentation depends on the context of usage: For inferential statistics, I find this simple reformulation orders of magnitude more useful. For an introductory course in probability theory, maybe not so much? Unfortunately, people will often take the introductory course first and then find that the follow-up course asks them to simply import the contents of that course into the new context.