One of my favorite tools from the Unity engine is the animation curve. Animation curves allow you to easily specify (mathematical) functions restricted to an interval. As an example, consider this declaration:
public class Example : MonoBehaviour {
public AnimationCurve Curve;
}
In the Unity editor, you get a very neat inspector for the animation curve:
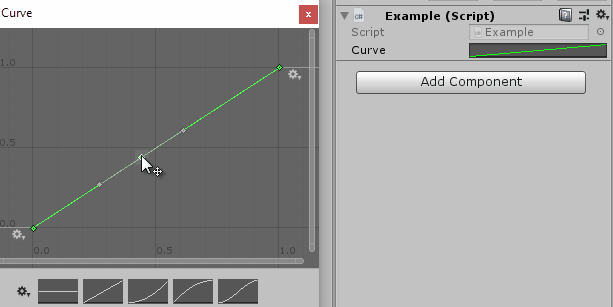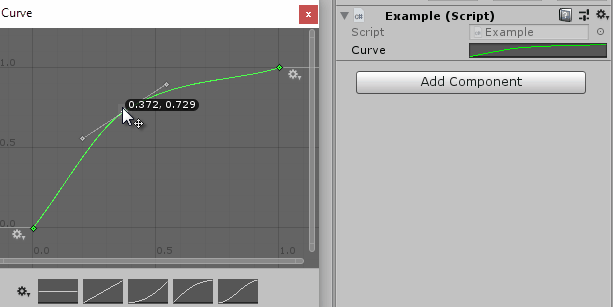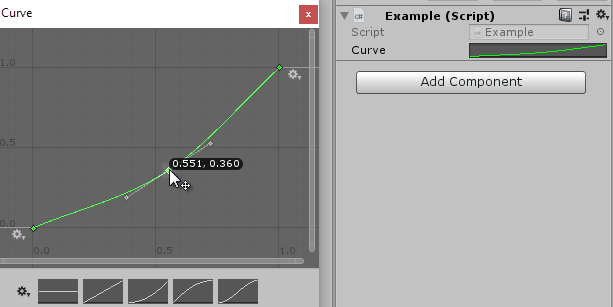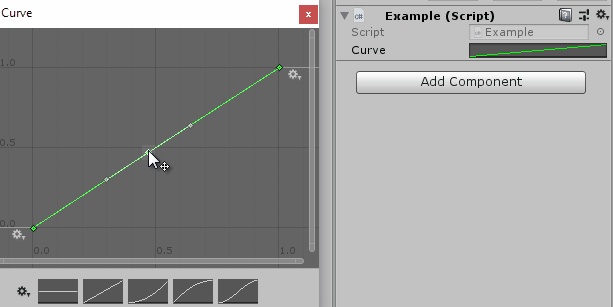
You can then use the Evaluate method to get the function value corresponding to the given input value. The editing may seem magical, but ultimately it is just a very nicely made tool to create a function from splines. Even though it is called an animation curve, there is no saying that you actually need to use it for animations – quite the opposite: Most of my uses for animation curves are not, in fact, related to animations!
Today, I’d like to highlight my favorite use of animation curves yet: Sampling.
Animation Curves as Probability Densities
My Unity projects often involve a degree of randomness. Many people automatically take random values to mean uniformly distributed random values, if only because they only know how to sample uniformly at random (in Unity, that means just using Random.value). There are various ways to sample from other well-known distributions, but in general I find it very hard to communicate to a designer what exactly they should expect when they are using an exponential distribution or $beta$-distribution. Animation curves give us an easy way to specify the (unnormalized) density functions for arbitrary distributions (on a finite-length interval, at least). As an example, this is a distribution on $[0, 1)$ in which extreme are very likely and there is a fair chance for values around 0.4, but other values are pretty unlikely:
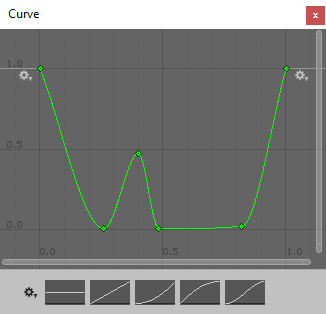
Such probability density functions are very easy to interpret: Large $y$ values mean that the corresponding $x$ values are very likely.
How do you sample from this distribution? There is a neat trick that made me feel very clever when I thought about it a few years ago (and significantly less clever once I found out that it is a pretty standard method to use). The basic idea is as follows: Instead of starting from scratch, assume that you have a way to sample a random value from $[0, 1)$ (and thus from any interval $[a, b)$ by scaling and shifting). When you are now given any (differentiable) monotone function $f$ with image $[a, b[$, you can easily build a sampler for $f’$, the first derivative of $f$. Imagine a line plot of $f$ (as in the animation curve editor) and shoot a horizontal ray from the $y$-axis at a point chosen uniformly at random using the sampler you already have. Note where it hits the function line and take the corresponding $x$-value. The probability of getting a specific $x$ value is completely dependent on the value $f’(x)$: If $f’(x) = 0$, then you will never hit that value. The larger the value $f’(x)$, the larger the slope of $f$ will be and it is not hard to see that this way you will actually sample according to $f’$ as a density.
This then allows us to build a sampler for an animation curve (it takes the role of $f’$) using the following strategy: First, integrate it (this constructs $f$) and then invert it (this allows us to convert our randomly sampled $y$ values to $x$ values) to get $f^{-1}$. The transform your uniform random sample with $f^{-1}$.
Both integration and inversion can be done numerically. The integration is implemented using a simple trapezoid method; inverting a monotone function is little more than a binary search. Here is the class that deals with the integration. It stores an array of intermediate values of the integral and interpolates between them to quickly produce an approximation to the integral up to a specific point:
using UnityEngine;
/// <summary>
/// Provides a numerically integrated version of a function.
/// </summary>
public class IntegrateFunc {
private System.Func<float, float> _func;
private float[] _values;
private float _from, _to;
/// <summary>
/// Integrates a function on an interval. Use the steps parameter to control
/// the precision of the numerical integration. Larger step values lead to
/// better precision.
/// </summary>
public IntegrateFunc(System.Func<float, float> func,
float from, float to, int steps) {
_values = new float[steps + 1];
_func = func;
_from = from;
_to = to;
ComputeValues();
}
private void ComputeValues() {
int n = _values.Length;
float segment = (_to - _from) / (n - 1);
float lastY = _func(_from);
float sum = 0;
_values[0] = 0;
for (int i = 1; i < n; i++) {
float x = _from + i * segment;
float nextY = _func(x);
sum += segment * (nextY + lastY) / 2;
lastY = nextY;
_values[i] = sum;
}
}
/// <summary>
/// Evaluates the integrated function at any point in the interval.
/// </summary>
public float Evaluate(float x) {
Debug.Assert(_from <= x && x <= _to);
float t = Mathf.InverseLerp(_from, _to, x);
int lower = (int) (t * _values.Length);
int upper = (int) (t * _values.Length + .5f);
if (lower == upper || upper >= _values.Length)
return _values[lower];
float innerT = Mathf.InverseLerp(lower, upper, t * _values.Length);
return (1 - innerT) * _values[lower] + innerT * _values[upper];
}
/// <summary>
/// Returns the total value integrated over the whole interval.
/// </summary>
public float Total {
get {
return _values[_values.Length - 1];
}
}
}
This function is then used in the AnimationCurveSampler which handles both the sampling and the inversion:
using UnityEngine;
/// <summary>
/// Samples according to a density given by an animation curve.
/// This assumes that the animation curve is non-negative everywhere.
/// </summary>
public class AnimationCurveSampler {
private readonly AnimationCurve _densityCurve;
private readonly IntegrateFunc _integratedDensity;
public AnimationCurveSampler(AnimationCurve curve, int integrationSteps=100) {
_densityCurve = curve;
_integratedDensity = new IntegrateFunc(curve.Evaluate,
curve.keys[0].time,
curve.keys[curve.length - 1].time,
integrationSteps);
}
/// <summary>
/// Takes a value s in [0, 1], scales it up to the interval
/// [0, totalIntegratedValue] and computes its inverse.
/// </summary>
private float Invert(float s) {
s *= _integratedDensity.Total;
float lower = MinT;
float upper = MaxT;
const float precision = 0.00001f;
while (upper - lower > precision) {
float mid = (lower + upper) / 2f;
float d = _integratedDensity.Evaluate(mid);
if (d > s) {
upper = mid;
} else if (d < s) {
lower = mid;
} else {
// unlikely :)
return mid;
}
}
return (lower + upper) / 2f;
}
public float TransformUnit(float unitValue) {
return Invert(unitValue);
}
public float Sample() {
return Invert(Random.value);
}
private float MinT {
get { return _densityCurve.keys[0].time; }
}
private float MaxT {
get { return _densityCurve.keys[_densityCurve.length - 1].time; }
}
}
Now it is straight-forward to treat an animation curve as a probability density function:
public class Example : MonoBehaviour {
public AnimationCurve Curve;
private AnimationCurveSampler _sampler;
private void Awake() {
_sampler = new AnimationCurveSampler(Curve);
// use this to sample according to the density given by the curve:
_sampler.Sample();
}
}